Mathematical Structure and Error in Kindergarten

You are here
There’s a growing literature on using children’s “misconceptions” to diagnose their thinking and to target interventions. While contributing to that literature, this article focuses on choices educators make and draws attention to a little-recognized benefit of children’s errors—errors can reveal strengths worth preserving, not just weaknesses to fix. With stories of two children, this article shows how wrong answers can reveal children’s attention to mathematical structure (NGA & CCSSO 2010). It also looks at how young children use patterns in language to make mathematical meaning.
Children’s errors—To correct or not to correct?
Young children are remarkable at generalizing the information they gather. For example, they quickly find the pattern of adding s to make a noun plural; but this correct conclusion also produces errors like saying “foots” instead of “feet.” Similar situations arise frequently in mathematics too, and these errors can reveal not just what students don’t know, but also what they do know. Therefore, teachers can use children’s ability and inclination to generalize and find patterns as an ally in teaching.
In general, the most useful place to intervene—adding challenge, correcting errors, or calling for reflection— is where the child’s intellectual growth is currently most rapid. Where the child is working, that’s where the child’s attention is. Errors help us notice that place because they’re common when a child enters new intellectual territory and is actively building new ideas. Patterns of errors sometimes reveal correct structures that the child built but misapplied—structures to be preserved. Other times, they reveal incorrect structures built using correct principles.
Some errors, of course, are just slips, revealing nothing but a momentary lapse of attention. Should we correct them? That depends. If they hide a mathematical pattern from the child, correcting them removes a barrier. Or if such small slips are considerably more frequent for a particular child than for most others the same age, then the child might need help with directing attention, controlling impulses (perhaps just slowing down), or taking a second look. But in many cases, small slips are worth ignoring. Focusing on errors can be a distraction, drawing attention away from what the child is really working on and interfering with building and using more advanced ideas and structures. At those times, it is more useful to affirm and build on the correct part of a child’s work.
We, as educators, won’t always know exactly where a child’s intellectual focus is and when to intervene. Like all communication, teaching is complex. Fortunately, learning is robust and children are mostly resilient, so teachers can make slips and students will still learn well.
Ruth: Attending to structure but inventing an incorrect one

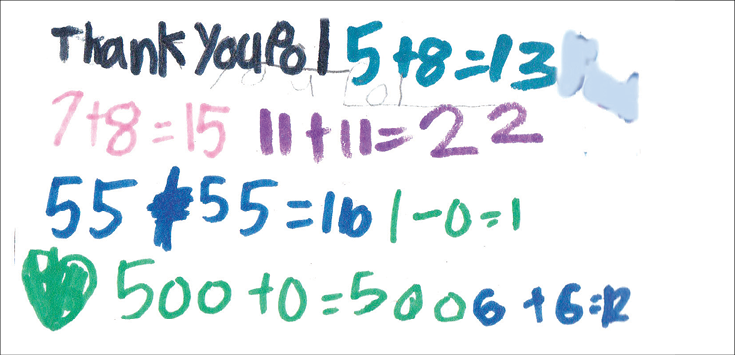
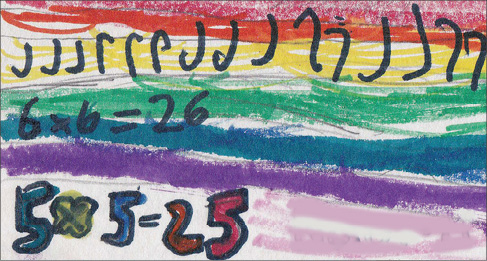
At the very end of kindergarten, a year in which the children learned about addition and subtraction, the children all create small thank-you cards for a regular visitor. Seth (top) draws a blue square with what looks like a red lollipop stuck to it, his representation of a wonderful logic puzzle. Many of the children entirely fill their cards with arithmetic of the sort they had been doing during the year, with some artistic elements and often with surprising extensions that they felt particularly good about. Sara (middle) adds a heart.
Six-year-old Ruth (bottom) creates this striking card with the math sentence 5 x 5 = 25 prominently displayed. The class didn’t study multiplication, but children pick up stray knowledge and love to show what they know. It’s not likely that Ruth knows yet what 5 x 5 = 25 means, but it’s fun to show off such a grown-up thing.
Ruth’s card is a rainbow of colors, leaving deliberate space for her elaborately written 5 x 5 = 25. A complex pattern runs across the top. The card is already so full that there isn’t room for more, but just above the 5 x 5 = 25, she crams in 6 x 6 = 26, seemingly as an afterthought and perhaps a spur-of-the-moment idea.
How perfect! If five times five is twenty-five, then six times six must be twenty-six.
That’s wrong, of course, but what we learn is that Ruth’s attention was on structure, not on random facts. Even though the structure she used is “wrong” (linguistic rather than mathematical), this is evidence of a fundamentally right idea about mathematics: she treated 6 x 6 not as another thing to remember, like the way she learns people’s names and the days of the week, but as something she could figure out. The way she figured it out wasn’t grounded in the meaning of multiplication—we could hardly expect that of a kindergartner—but it shows that she sees mathematics as nonarbitrary, something that can be figured out and that should make sense.
Having noticed Ruth’s error, what might her teacher do? Three reasonable options would be (1) to tell Ruth that 6 x 6 = 36, (2) to show her what 5 x 5 means, and (3) to ignore it—after all, it is a drawing, not a math quiz. Ignoring it seems harmless. Ruth certainly doesn’t need correction right now; she’s not studying multiplication in kindergarten. And we need not worry that Ruth might, if uncorrected, memorize 6 x 6 = 26; if facts were that easily memorized, we’d all be ecstatic! Maybe telling her that the correct answer is 36 would also be harmless. Ruth is clearly a thinker, so she might seek a pattern in the new data and conclude that if five times five is twenty-five, and if six times six is thirty-six, then perhaps seven times seven is forty-seven. If she did, that would be another error, but no more harmful than the first. It would also be another example of Ruth seeking structure and (incorrectly) generalizing it.
Here’s the downside of correction. With no foundation to make sense of multiplication, telling Ruth that the correct answer is 36 would just give her another random fact. It wouldn’t aid her understanding of multiplication, and might harm her overall understanding of mathematics. Ruth tried to make mathematics make sense. If she is told “Nope, wrong answer” without the knowledge and logic to understand why, she might change her perception of mathematics and believe it to be arbitrary. Ruth perceived mathematics as being about finding pattern and structure, even if her limited knowledge leads her to a spurious pattern or the wrong structure. That is the right perception of mathematics, and we don’t want to change it. Someday Ruth will make sense of multiplication and use that understanding to come up with a better result for 6 x 6.
Focusing on errors can be a distraction, drawing attention away from what the child is really working on.
What about showing Ruth what 5 x 5 means? Without commenting on her error, the teacher could add meaning to Ruth’s correct statement by setting out dice while saying, “How cool! You’ve told us about five fives! Here’s a five, now two times, now three times, now four times, now five times. Twenty-five!
The teacher could stop there, without teaching multiplication. The dice would let Ruth see what her idea means, using a familiar image of 5 and a quantity she can count. Ruth might follow up, or she might not. She might try something like on her own. She’s still not “studying multiplication” (she’ll count or add), but she can attach a new meaning to a fact she’s already proud of knowing. And if she does not follow up, no time has been wasted, and she has not been criticized on the wrong outcome of her wonderful pattern-finding or pushed beyond her interest.
So, when should a teacher make sure children know the correct answer? And when is it more important for children to focus on pattern and logic, even if the outcome isn’t accurate? It depends on where the child’s attention is—where the child is actively working. If Ruth’s error were related to concepts in which she was currently growing rapidly—addition and subtraction—it would be important to determine whether the mistake was systematic or just a slip. If systematic, her teacher might want to intervene. If just a slip, then asking Ruth to check two results (one correct, one wrong) to see if she can catch and fix the error herself might be sufficient. Still, correction is an option; we might decide that Ruth’s time would be better spent on something else.
Linguistic patterns, mathematical learning
Ruth’s invention of 6 x 6 = 26 illustrates a useful truth about young children’s mathematical learning. It’s connected to their learning of spoken language.
Children—especially young ones—are superheroes at language learning, many learning 10,000 or more vocabulary items in the first five years of life and developing a nearly complete structure (grammar) for their language before they reach kindergarten. This is a fact that even their errors reveal: they’ll say “I goed outside,” inventing an incorrect word by applying a correct rule that they themselves generalized. They also actively build many other kinds of structures, including categories (elephants and cats are different from chairs and tables) and subcategories (they find the concept of a pet elephant funny but don’t know what to make of a pet chair). They love to count things and compare sizes. Young children’s experiences are a riot of near-constant newness, and children are rapidly building new structures to organize them.
Children apply structures they’ve already built, like the structure of their spoken language, to help sort out newer ideas, like mathematics or writing. Given the chance to experience mathematics verbally and not  just in writing, they use their expertise at finding structure in language as a base for mathematical learning. For example, young children readily connect six, seven, and eight with sixty, seventy, and eighty, and learn the pattern (if not yet the meaning). They also connect that pattern with number names like sixty-one, seventy-one, eighty-one, and so on.
just in writing, they use their expertise at finding structure in language as a base for mathematical learning. For example, young children readily connect six, seven, and eight with sixty, seventy, and eighty, and learn the pattern (if not yet the meaning). They also connect that pattern with number names like sixty-one, seventy-one, eighty-one, and so on.
Teaching can capitalize on the fact that the spoken language of number can be such a strong support for mathematical learning, especially in the early grades, and can expose young children’s mathematical abilities that remain hidden when the approach is largely through writing. A recent discussion with a different kindergarten class provided an excellent example. To probe the children’s thinking, one of the authors asked them to name the biggest number they could think of. Most said things like “a hundred” or “a million.” Nobody said things like “two hundred” or “seven million.” But when we asked what they supposed two hundred plus three hundred might be, almost all readily answered five hundred. To better understand their responses, we asked another question: “What do you think a hundred plus a hundred is"? This question, which seems simpler, proved more of a puzzle for the children. Though some said two hundred, several gave other answers, like “a hundred,” “a million,” and “I have no idea,” even though just moments before they had correctly added to find five hundred!
This paradox vanishes when we figure out what’s really going on in their bright, active minds. The child who said “a hundred plus a hundred is a hundred,” interpreted hundred to mean “big number.” Given that, his statement was perfectly correct: a big number plus a big number is a big number! The child who responded “a million” was saying that a big number plus a big number is a bigger number. In contrast, adding two hundred plus three hundred is a linguistic act to which the children applied their knowledge of 2 + 3. (It reminds us of a child who, when asked what five-eighths plus five-eighths was, confidently answered “Ten ayfs! What’s an ayf"?) Though hundred just meant “big number,” the children were processing “two hundred plus three hundred” the way they’d process “two goats plus three goats.” The numberness of hundred was not really used; most of the children seemed to have only a vague idea about it as a quantity and maybe not even complete certainty that it was a specific number. (Similarly, in grade 1 or 2, many children who know that half of eight is four confidently assert that half of eight million is four million and half of eighty is forty, if these are spoken computations. The children may not yet have a solid mathematical concept of those numbers—for that matter, few adults have a clear picture of exactly how huge a million really is—but making verbal sense of manipulating large numbers in this way helps children when they later formalize their structure and notation.)
While kindergartners have little to no concept of a million as a number, Ruth and her classmates had gotten lots of experience counting, investing precision in the initially vague meanings they had for counting words. The counting words they used and their experiences building the number hundred from 10s gave at least partial meaning to these numbers and to addition. Importantly, the linguistic patterns they started with provided a structure for their counting. Language and mathematical meaning codeveloped, each supporting the other.
Ruth’s “6 x 6 26” comes from a (wrong) use of linguistic pattern; but the attention she and her classmates give to linguistic patterns in number names, along with the experience they gain using that language in context, allows them to do—with understanding and competence and confidence—many mathematical things not usually expected in kindergarten. (For more about how mathematical habits of mind relate to language, see Goldenberg, Shteingold, & Feurzeig 2003.)
Sonya: Basing a correct structure on an incorrect first step
 Sonya, one of Ruth’s classmates, is a solid reader and a strong arithmetician. Her mental computation by the end of kindergarten would delight a first grade teacher. She is a tenacious puzzle solver, able to hold a fairly complicated set of puzzle constraints in her head. She is used to getting right answers quickly; but when she does make a mistake, she (like most young children) is not yet self-reflective enough to notice and correct it.
Sonya, one of Ruth’s classmates, is a solid reader and a strong arithmetician. Her mental computation by the end of kindergarten would delight a first grade teacher. She is a tenacious puzzle solver, able to hold a fairly complicated set of puzzle constraints in her head. She is used to getting right answers quickly; but when she does make a mistake, she (like most young children) is not yet self-reflective enough to notice and correct it.
One activity in Sonya’s math book asks that she pick a starting number, roll a die, add that number to her selected number, and write the result. On the next line, she is to start with that result, roll and add again, and write the new result. And so on. For Sonya, this is a familiar activity; she chooses 24 to start. She rolls the die. She likes getting the biggest number, so she changes her die roll to 6 . She counts up from 24 and gets 30. But then, as is common with children (even at 8 or 9 years of age and even with adults, if the task is taxing enough), she gets distracted by the starting place she is keeping in her head—24—and writes 34 instead of 30.
Sonya already knows that if she repeats an addition that got her from 24 to 34, it will get her from 34 to 44, then to 54, then 64. Having shown her mathematical strength throughout the year, she clearly knows (and says) that to get from 34 to 44 you must add 10, not 6. She also shows facility with the sequence of 10s and with pairs like 4 + 6 that make 10. In this instance, she has correctly counted to 30—but noticing her slip of writing 34 is another story. And using her knowledge to catch the slip would require a self-reflective slowness that is rare among kindergartners. So, when she rolls the die a second time and again changes it to get 6, she just continues her pattern without a moment’s thought.
The last line on her activity sheet shows the same kind of (super common!) slip she started with. Sonya meant to write 64, got distracted by her starting number, 54, and wrote 54 instead. This time, she did spontaneously catch and correct her slip.
So, should her teacher point out the other errors? There are both nonmathematical and mathematical issues to consider.
›› Nonmathematical considerations: Sonya filled in the page wrong, every line of it. Children should learn that just writing stuff on a page is not the goal. And if the paper will be seen by parents or others, it should not look like the child was slapdash and the teacher didn’t even notice. Correction can come without fuss. Sonya might even enjoy seeing the “oops” and fixing everything in order to have a perfect paper to show. And seeing that what she wrote is not what she knows might help her become more careful. Such self-monitoring is rare at this age. Is it learnable for this child at this time, or is intervention before more maturity just wasteful and distracting?
›› Mathematical considerations: Was this error at Sonya’s growing edge? Yes. Her current intellectual focus is on structure in addition. What did Sonya’s error reveal about her thinking? It showed that she’s mathematically reflective; rather than just moving on, she noticed her first result. She did not notice that it was wrong, but she did notice the increase by 10 and applied that structure. Many of her earlier lessons and activities indicate that the error was just a slip, not a mathematical misunderstanding. Sonya has nothing mathematical to learn from correcting this mistake.
We have choices about where to focus and about whether and when to correct.
So, should Sonya be corrected? This is where teacher judgment is important. There’s no general answer. Happily, a general answer is not needed. We teachers teach specific children, not general ones— specific children with specific strengths and specific relationships with their teachers. As in all human interaction, we make a guess—but an educated one. And we watch. If Sonya’s teacher misses the mark, she might try again using a different strategy. Or we wait. Not everything needs to be corrected; and not everything that does need to be corrected needs to be corrected immediately. (For two stories about how what appear to be errors can indicate deep understanding, see Goldenberg 2017.)
Focus on structure versus focus on accuracy
No, not versus! That’s the point. We have choices about where to focus and about whether and when to correct. In fact, this is very familiar to many early childhood teachers for subjects other than mathematics—for example, teaching young children to write. At first, letter reversals, seemingly random capitalization, and lack of punctuation are not a great concern; grasping the concept of representing words with letters is the primary goal. Invented spellings are evidence that children have moved beyond the random letter-spray of preschool and have grasped that the letters one uses to write a word should be related to the sounds of the words. Choosing what to emphasize and when is a big part of teaching.
In mathematics, teachers often seem more reluctant to make such choices. Maybe that is because so many people (including teachers, administrators, and parents) believe that the final written answer is the measure of mathematics learning—after all, even if your thinking is perfect, the bridge collapses if you write the wrong number at the end. Or maybe it is because, unlike in a piece of writing, we often do not see a story in the math, just a final number; so, if it is wrong, well, it is wrong. But the work of Sonya and Ruth shows how even a single number can sometimes tell a story.
Conclusion
Accuracy matters, but not always. How do we teachers know when to correct or where to focus? We won’t always choose perfectly—there may not even be a choice with no risks. As long as teachers are thinking about whether or not to correct and what is communicated with that correction, as long as they are deciding what to do and not simply reacting to what was written, as long as they are considering the particular child, they increase their chances of making a good instructional decision.
Sonya’s teacher chose not to correct her. In that instance, supporting Sonya’s inclination to use a pattern seemed more helpful for Sonya’s mathematical development than drawing her attention to incorrect results. It is not possible to know for sure whether pointing out the slip might have had a better outcome. Fortunately, children and circumstances provide corrective feedback over time. Like Sonya, who will get other chances to add more accurately, we teachers too will get other chances to decide what responses are best. As long as teachers are guided by thoughtful responses, they build models about each child’s learning that help guide interactions far better than any generic list of do's and don’ts could.
Authors’ note: The work reported here was funded in part by The National Science Foundation (award numbers 1119163 and 1348564) and by the Heising-Simons Foundation (award number 2015-023). Views expressed here are the authors’ and do not necessarily reflect the views of the foundations.
More for the Interested Teacher
Hansen, A., ed. 2014. Children’s Errors in Mathematics. 3rd ed. Exeter, UK: Learning Matters.
Ryan, J., & J. Williams. 2007. Children’s Mathematics, 4–15: Learning from Errors and Misconceptions.
References
Goldenberg, E.P., N. Shteingold, & N. Feurzeig. 2003. “Mathematical Habits of Mind.” In Teaching Mathematics through Problem Solving: Prekindergarten–Grade 6, ed. F.K. Lester. Reston, VA: National Council of Teachers of Mathematics.
Goldenberg, E.P. 2017. “Correct Answer/Wrong Question: Theory of Mind in a Mathematics Class.” EDC Learning and Teaching Blog, Jan. 6. http://ltd.edc.org/wrong-answers-or-wrong-questions.
Hansen, A., ed. 2014. Children’s Errors in Mathematics. 3rd ed. Exeter, UK: Learning Matters.
NGA (National Governors Association) Center for Best Practices & CCSSO (Council of Chief State School Officers. 2010. “Look for and Make Use of Structure.” (CCSS.Math.Practice.MP7.) Common Core State Standards in Mathematics. Washington,DC: NGA & CCSSO. www.corestandards.org/Math/Practice/#CCSS.Math.Practice.MP7.
Ryan, J., & J. Williams. 2007. Children’s Mathematics, 4–15: Learning from Errors and Misconceptions. Berkshire, UK: Open University Press.
Photographs: 2, 4, courtesy of author; 1, 3, 5, © iStock
E. Paul Goldenberg has taught mathematics from early elementary through graduate school and now develops mathematics curriculum at Education Development Center (EDC), in Waltham, Massachusetts. He especially likes building mathematical connections and fostering students’ questions and problem posing leading to depth, surprise, and new ideas. [email protected]
Sharon J. Miller has taught kindergarten at The Rashi School, in Dedham, Massachusetts, for 18 years and has worked with young children for three decades. She enjoys helping students recognize and pursue mathematical sense through exploration and use of familiar and new materials. [email protected]
Cynthia J. Carter teaches mathematics in sixth, seventh, and eighth grades at The Rashi School. She especially loves helping students think like mathematicians, building systems and posing—as well as solving—problems. [email protected]
Kristen E. Reed, project director at EDC, has worked as a teacher, curriculum developer, professional development facilitator, and researcher. For more ways to make math engaging, challenging, and fun, visit ym.edc.org. [email protected]